Editor’s note: This blog post was first published by Partnership Schools.
We recently shared this captivating clip of Our Lady Queen of Angels’s Kindergartener Iliana C. teaching her mom number bonds and sentences.
Now you’re probably gushing over Iliana’s natural born teaching technique like we were. But we think this clip is doubly powerful because it subtly reveals what is happening behind the scenes. That is, for every vibrantly engaged Iliana “doing math” (and loving it), there is a devoted teacher like Yasmin Camacho behind them, ensuring her students make the most of these dog days of distance learning.
To maximize the time our students spend on math at home, Partnership Schools teachers have tailored their remote instruction in different ways, depending on the grade level.
- In the early elementary grades, teachers continue to lay the foundation of number sense, numeration, and basic operations that our youngest scholars will need for the next levels of math that await them when they return to school.
- In upper elementary and middle school, we emphasize procedural fluency—a prerequisite to the higher math we want to ensure students are prepared for.
- Across all grades, teachers create regular opportunities for students to speak and write in the language of mathematics.
The examples below are a window into how these approaches look in practice.
On prioritizing number sense and numeration in pre-K–2
Just as we teach early readers that we use symbols to represent sounds in reading, our young mathematicians must learn how symbols represent quantities. Early number sense involves making comparisons between numbers, estimating, and understanding concepts like longer and shorter, more and less, height and width.
Working towards this, Saramarie Colandra warms up her pre-kindergarteners with numeration practice and then shifts to building knowledge about length using manipulatives she knows they can readily find around the house—crayons and Cheerios.
Similarly, kindergarten teacher Leslie Ciancuillo rolls out basic subtraction “number sentences.” Students start with pennies as manipulatives and then she gradually adds complexity by requiring them to draw their own representations of quantities as boxes. She’s explicit about building students’ association between the minus sign and the operation of subtraction. Topping it all off, Leslie makes sure her students rehearse reading their number sentences aloud to help ingrain their new vocabulary in memory.
Imalai Castro reviews arrays with her second graders—a strategy used to help student visualize multiplication. Imalai knows it is critical to reinforce key vocabulary like columns and rows. And we’re smitten with how she leverages students’ knowledge of architecture in Ancient Greece as a reference point. (Thank you, CKLA!)
On building procedural fluency
In upper grades, our teachers have focused on procedural fluency, knowing that it sets the stage for engagement with higher math. This means building long-term memory of math knowledge of facts and algorithms. But it also involves developing students’ ability to perform accurate computations speedily and consistently, learning to nimbly apply their knowledge to different types of problems.
Watch fourth grade teacher Kat Prevo model a method for decomposing mixed numbers into improper fractions. Her modeling is incredibly disciplined, and her voiceover of each step is thoughtfully preplanned and precise. This helps to guard against students getting confused or distracted by unintentional variations.
She also provides a robust set of sample problems to inculcate the procedure. She promotes active engagement in her model by prompting students with thinking tasks: “I want you to be thinking of why I would want to multiple three wholes with four fourths.” And after several thoroughly explained examples, she gradually releases more computation work to students (at eleven minutes), tasking them with certain steps before checking their work against hers.
Seventh grade teacher Julie Ficuciello adapts the same strategic modeling approach to paper. Check out the materials she’s created for students below. She’s included two model problems with clear exemplars for students to reference, alongside two problems for them to try independently and submit back to her for feedback.
She’s also anticipated how students will struggle and provided some hints at the very bottom of the document, scaffolding their work should they need the extra support. (See Julie’s student work packet for more.)
On using the language of math
While our students can’t engage in discussion as they normally would in the classroom, our teachers have still tasked students with communicating mathematical ideas. As our elementary teachers have demonstrated, this can be as simple as asking students to read a number sentence aloud or describe a procedure to an adult at home. But they’ve also continued to prepare older students—our eighth graders, especially—for the more sophisticated math discourse they’ll encounter in high school.
Julie Ficuciello requires her students to write about math concepts several times a week. This ensures they have understood and can articulate the conceptual underpinnings, or “big ideas,” of her lessons.
Julie recently posed this question and students sent her a snapshot of their responses: “Why is it necessary to establish a correspondence when comparing two triangles?” Take a peek at a couple of their responses:

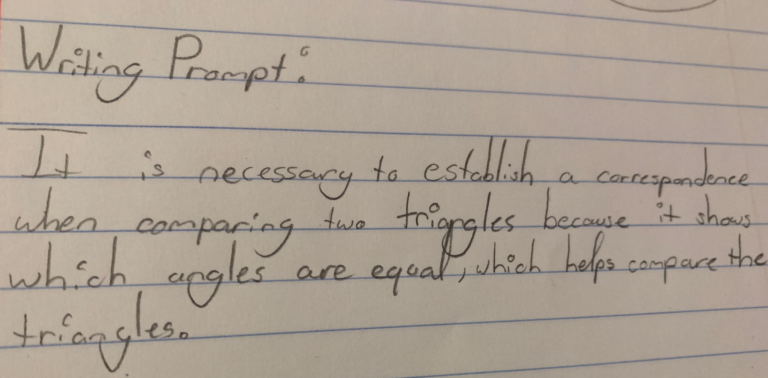
Julie proves that keeping the rigor high doesn’t require us to go high-tech.
Of course, what our teachers are focusing on may be just as important as what they aren’t. For now, we’ve deprioritized the more abstract work intended to build conceptual understanding. We agree that this work holds much value. It helps students see math as more than a set of facts and procedures. But this moment calls for us to minimize frustration and maximize what our students yield from independent, distance learning.
That means keeping them “doing math,” as much as we can.
As the great, contemporary mathematician Paul Halmos said: “The only way to learn mathematics is to do mathematics.”




